Logické funkcie s niekoľkými premennými

Tie opisujú riadiacu funkciu, ktorú má zabezpečovať riadiace zariadenie. Zostavujú sa zo slovnej formulácie úlohy, ktorú majú plniť. Takto zostavená funkcia je obvykle zložitá. Logický obvod navrhnutý podľa nej by bol zbytočne zložitý. Preto takúto funkciu treba zjednodušiť - minimalizovať. Naučíme sa funkcie minimalizovať na základe zákonov a pravidiel Booleovej algebry a pomocou Kamaughovej (Karnafovej) mapy. Minimálna forma funkcie je taká, ktorá sa už ďalej nedá minimalizovať.
Zákony Booleovej algebry:
Zákon komutatívny:
F = A + B = B + A
F = A . B = B . A
V konjunkcii aj v disjunkcii môžeme poradie premenných zameniť a hodnota funkcie sa nezmení.
Zákon asociatívny:
F = A + B + C = B + (A + C) = C + (A + B)
F = A . B . C = B . (A . C) = C . (A . B)
V konjunkcii aj v disjunkcii môžeme ľubovoľné dve premenné uzavrieť do zátvoriek a hodnota funkcie sa nezmení.
Zákon distributívny:
Tento zákon pojednáva o vyňatí pred zátvorku alebo o roznásobení zátvorky.
F = A . B + A . C = A . (B + C)
Z disjunkcie dvoch konjunkcii môžeme spoločnú premennú vyňať pred zátvorku.
F = (A + B) . (A + C) = A + (B . C)
Z konjunkcie dvoch disjunkcii môžeme spoločnú premennú vyňať pred zátvorku.
Pravidlá Booleovej algebry:
Pravidlo neutrálnosti konštánt:
A . 1 = A
A + 0 = A
Konštanta nemá žiadny vplyv na premennú.
Pravidlo agresívnosti konštánt:
A . 0 = 0
A + l = l
Premenná je konštantou pohltená.
Vzťah medzi premennou v pozitívnom a negovanom tvare:
A + A = 1
A . A = 0
Pravidlo absorpcie:
A . A . A ... = A
A + A + A ... = A
Ak je v konjunkcii alebo disjunkcii viac ráz tá istá premenná, uvažujeme s ňou len raz. Na základe tohto pravidla si môžeme z jednej premennej namnožiť taký počet premenných, koľko ich potrebujeme pri ďalších úpravách.
Pravidlo o dvojnásobnej negácii:
A = A
--
Dvojnásobná negácia premennej je pôvodná premenná.
Pravidlo absorpcie negácie:
A + A . B = A + B
Pravidlá De Morganove:
A + B = A . B
A . B = A + B
Minimalizacia logických funkcii pomocou Karnaughovej mapy.
Poznáme Karnaughove mapy pre dve až šesť premenných.

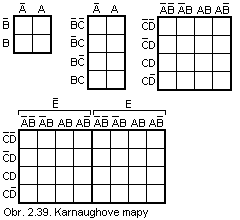
Namiesto premenných pred riadkami a nad stĺpcami sa môžu písať konštanty 0,1. Mapa pre tri premenné vznikne spojením dvoch máp pre dve premenné, podobne mapa pre štyri premenné vznikne spojením dvoch máp pre tri premenné atď. Štvorčeky nazývame polia, počet polí v mape je 2n, kde n je počet premenných. Počet polí v mape je zhodný s počtom riadkov v tabuľke stavov.
Minimalizácia Karnaughovou mapou je založená na opakovanom používaní pravidla A + A = 1 pre susedné polia v riadku alebo v stĺpci. Susedné stĺpce alebo riadky sa vždy líšia v hodnote jednej premennej.
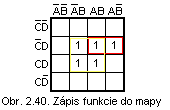
Funkciu F = ABCD + ABCD + ABCD + ABCD + ABCD zapíšeme do mapy tak, že do priesečného poľa riadka so stĺpcom zapíšeme symbol 1 pre každú konjunkciu z funkcie. Takto zapíšeme všetky konjunkcie, ktoré sa vo funkcii vyskytujú. Polia s 1 spojíme do blokov (uzavrieme do slučiek).

Tvorba blokov:
počet polí v bloku je mocninou čísla 2,
bloky môžeme tvoriť len v smere riadkov alebo stĺpcov, ale nie šikmo (v smere diagonál),
tvoríme čo najväčšie bloky,
bloky sa môžu prekrývať.

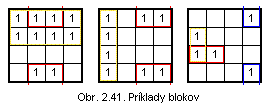
Vypisujeme tie premenné, ktoré sa pozdĺž strán bloku nemenia. Premenné z jedného bloku tvoria spolu konjunkciu, ak je v mape viac blokov, tak konjunkcie navzájom tvoria disjunkciu.
Funkcia vypísaná z mapy podľa obr. 2.40. je: F = BD + ACD.