2.3. Logické funkcie

Logická funkcia je predpis, ktorý kombinácii n-vstupných premenných A, B, C, ... jednoznačne priraďuje hodnoty výstupnej (závislej) premennej F.
Premenná podobne ako signál môže nadobúdať len dve hodnoty 0 a 1, teda sa nemôže spojite meniť. 0 a 1 sú logické konštanty.
Logickú funkciu môžeme zapísať pomocou funkčných rovníc, tabuľkou stavov alebo medzinárodným slovným symbolom.
Príklad: F = A • B je zápis funkcie logického súčinu (konjunkcie).
Slovné vyjadrenie funkcie má charakter výroku s použitím slovného symbolu:
„F je 1 (F = 1), ak A je 1 (A = 1) aj (und, and, ...) B je 1 (B = 1)."
Tabuľka stavov má ľavú a pravú časť. V ľavej časti sú v záhlaví uvedené všetky premenné a pod nimi všetky kombinácie ich hodnôt. V pravej časti je symbol výstupnej premennej a jej hodnoty pre každú kombináciu vstupných premenných.
Poznámka: Ľavú časť tabuľky vyplníme ľahko, ak si predstavíme, že konštanty v jednotlivých stĺpcoch sa striedajú s mocninou 2. Ak ideme sprava doľava, tak prvý stĺpec je 2⁰ = 1, striedanie je 0, 1, 0, 1,...
Druhý stĺpec je 2¹ = 2, striedanie je 0, 0, 1, 1, 0, 0, 1, 1,...
Otázka: Aké by bolo striedanie, keby tabuľka mala 5 vstupných premenných?
Nakreslite tabuľku!

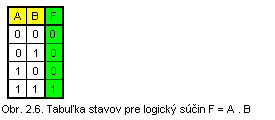
Rozdelenie funkcií podľa počtu premenných:
- funkcie s jednou premennou,
- funkcie s dvoma premennými,
- funkcie s viacerými premennými.
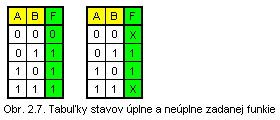
Zadanie logickej funkcie. Logická funkcia môže byť zadaná úplne, t.j. je známa hodnota funkcie pre všetky kombinácie vstupných premenných. Ak je hodnota funkcie pre niektoré kombinácie vstupných premenných ľubovoľná, alebo nie je určená, potom je funkcia zadaná neúplné.
Logické funkcie s jednou vstupnou premennou.

Sú to funkcie s jednou nezávislou premennou.
Funkcia F₂ = A je funkcia opakovacia, funkcia F_l = A je negácia vstupnej premennej.